【算法】滑动窗口和前缀和

算法
,

遇到了题目 437.路径总和 III ，学习一下滑动窗口和前缀和。重点是前缀和。

滑动窗口

参考链接：

滑动窗口主要用来处理连续问题。比如题目求解“连续子串 xxxx”，“连续子数组 xxxx”，就应该可以想到滑动窗口。能不能解决另说，但是这种敏感性还是要有的。

模版代码

给出窗口指针 left，right 表示窗口的左右顶点。

固定窗口代码模版

  1. left 初始化为 0

  2. 初始化 right，使得 right - left + 1 等于初始窗口大小

  3. 同时移动 left 和 right

  4. 判断窗口内的连续元素是否满足题目限定的条件

    • 4.1 如果满足，再判断是否需要更新最优解，如果需要则更新最优解

    • 4.2 如果不满足，则继续。

可变窗口代码模版

  1. left 和 right 初始化为 0

  2. r 指针移动一步

  3. 判断窗口内的连续元素是否满足题目限定的条件

    • 3.1 如果满足，再判断是否需要更新最优解，如果需要则更新最优解。并尝试通过移动 l 指针缩小窗口大小。循环执行 3.1

    • 3.2 如果不满足，则继续。

例题

https://leetcode.cn/problems/minimum-size-subarray-sum/solution/chang-du-zui-xiao-de-zi-shu-zu-by-leetcode-solutio/


前缀和

参考链接：

问题引入

思考一个问题：求一个数组的所有连续子数组。

连续子数组指的是索引连续的子数组。例如，数组 [1,3,4] 的连续子数组包括 [1], [3], [4], [1,3], [3,4], [1,3,4] 。

其中一种思路是，令 $ f(i) $ 表示以索引 $ i $ 结尾的子数组的个数。那么显然，子数组的总个数就等于 $ \sum\limits_{i=0}^{n-1}f(i) $ （n 表示数组长度）。同时，我们也能发现，$ f(i+1) = f(i) + 1 $ 。

这里我们就发现了前缀的概念：如果我们能够求出以索引 i 结尾的所有子数组，那么我们就能顺利地求出以 i+1 结尾的所有子数组。

例题

leetcode 437.路径总和 III

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

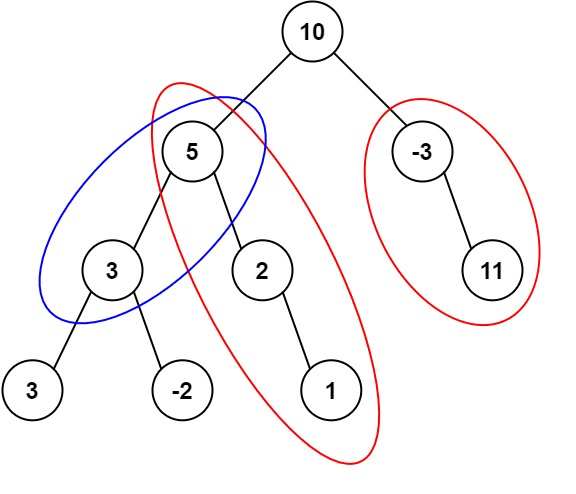
Untitled

1
2
3
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

1
2
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

思路：

该问题同样满足前缀和。以示例 1 的树为例，我们考虑以结点 5 为结束结点的路径，显然有 [10,5] 和 [5] 。此时，我们很容易得知，以结点 3 为结束结点的路径有：

  • [10, 5, 3] = [10, 5] + 3

  • [5, 3] = [5] + 3

  • [3]

因此，只要我们得到了以父结点为结尾的路径，我们能立刻得到以其子结点为结尾的路径。根据这种思路，采用先根序遍历树即可得到所有路径。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
        self.answer = 0
        self.target = targetSum
        self.backtrack(root, [])
        return self.answer

    def backtrack(self, node, paths):
        # paths 保存的是以 node 结尾的路径，其结点的值之和
        if node is None:
            return
        
        # 先根序
        paths.append(0)
        paths = list(map(lambda x: x+node.val, paths))
        self.answer += paths.count(self.target)

        self.backtrack(node.left, paths[:])
        self.backtrack(node.right, paths[:])