【算法】最小生成树

算法
,

题目链接：https://leetcode.cn/problems/min-cost-to-connect-all-points/

对于本题，可以视作所有的点之间都联通，构成一张图。然后生成图的最小生成树。

我记得在计算机网络还是数据结构课上讲过，可惜已经全忘了。来复习一下。

最小生成树算法有 Kruskal (克鲁斯卡尔算法) 和 Prim (普里姆算法) 等。

Kruskal 算法

基本思想：从小到大加入边，本质上是贪心算法。

流程：

  1. 将图 $ G= {V,E} $ 中的所有边按照长度从小到大排序；长度相等的边任意排序；

  2. 初始化图 $ G’={V, \varnothing } $ ，然后按顺序扫描长度从小到大的边，如果这条边能够使图 $ G’ $ 中的两个联通块相连，那么就将它插入到 $ G’ $ 中；

  3. 最终，生成的 $ G’ $ 就是 $ G $ 的最小生成树。

第二步中，判断两个结点各自所在的联通块是否相同，以及合并不同的两个联通块，显然是并查集的范畴。后面会复习一下并查集。

Prim 算法

待续。

附：并查集

参考链接：https://zhuanlan.zhihu.com/p/93647900/

并查集提供两个操作：

  1. 合并两个集合；

  2. 查询两个元素是否在同一个集合中。

问题定义

n 个元素存放在长度为 n 的数组 p 中。方便起见，记其中第 i 个元素为 i，即 p[i] = i 。

每个集合使用一棵树来表示，只不过这棵树的边是由子结点指向父结点的。树根结点的值也即是集合的编号。最初状态下，每个元素都分别属于一个集合。

合并操作

给出元素 x 和 元素 y，如果将 x 所在的元素集合合并到 y 所在的集合，需要先找到 x 所在集合的根结点（记作 z），然后令 p[z] = y 即可。

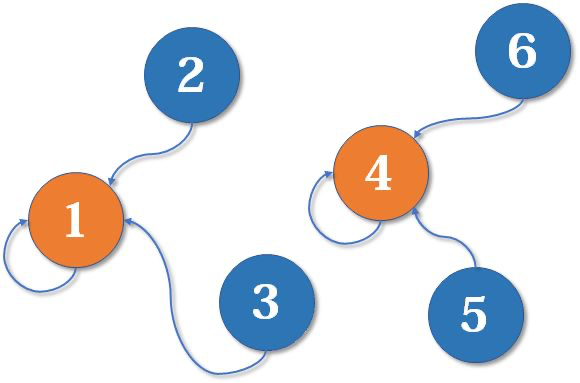
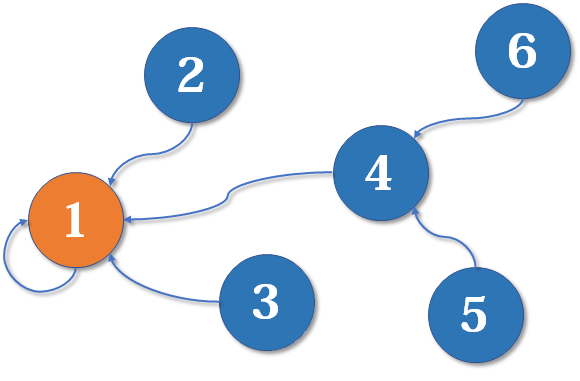
Untitled

Untitled

查询操作

给出元素 x 和 元素 y，只需要对比各自的根结点是否相同即可。

路径压缩

显然，树的深度越大查询的效率就越差。所以我们可以让树的所有子结点都直接指向根结点，以加快查询效率。

只要我们在查询的过程中，把沿途的每个节点的父节点都设为根节点即可。下一次再查询时，我们就可以省很多事。

按秩合并

在合并两个集合 x 和 y 时，应当把深度较小的树合并到深度较大的树上，如同下面这个例子：

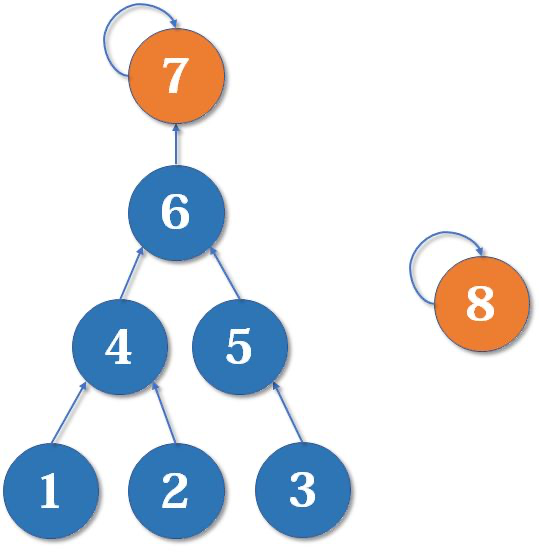
Untitled

对于 7，8 这两个元素，把 8 合并到 7 显然要由于反过来的情况。因为反之增加了树的深度。

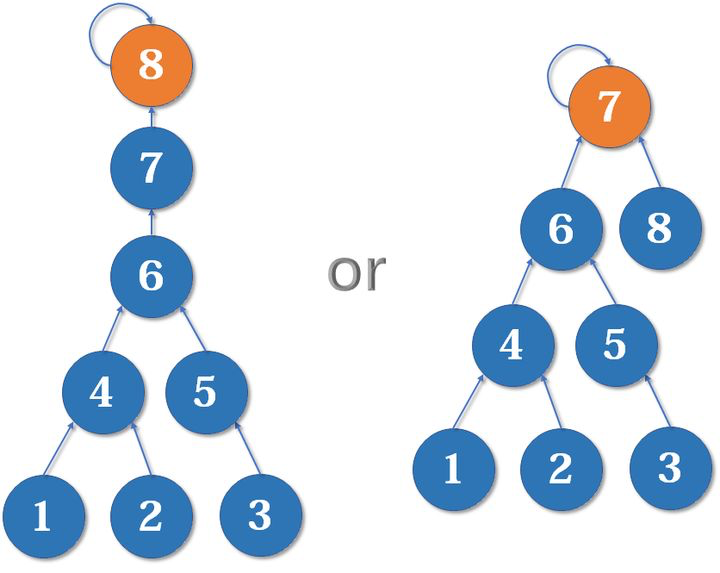
Untitled

因此，我们可以用一个额外的数组 rank 来记录每个根结点对应的树的深度（称为秩）。在合并时，将秩较小的树合并到秩较大的树。

最后的并查集代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class UnionFind:
    def __init__(self, n: int):
        self.p = [i for i in range(n)]
        self.rank = [1 for i in range(n)]
    
    def find(self, x, y):
        return self.getRoot(x) == self.getRoot(y)
    
    def union(self, x, y):
        xr = self.getRoot(x)
        yr = self.getRoot(y)
        if xr == yr:
            return False
        
        if self.rank[xr] < self.rank[yr]:
            self.p[xr] = yr
        else:
            self.p[yr] = xr
            self.rank[xr] = max(self.rank[yr] + 1, self.rank[xr])
        return True

    def getRoot(self, i):
        if self.p[i] == i:
            return i
        else:
            self.p[i] = self.getRoot(self.p[i])
            return self.p[i]